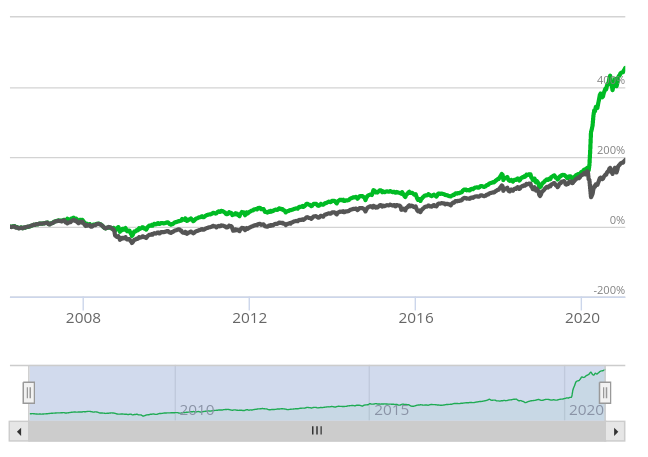
In my last post about hedging a portfolio with options, I looked at how a complicated 4-option spread could replicate the VIX index and hedge against market volatility. Now, we’re going to look at a simpler, explicit “tail risk” hedge using VIX calls. This strategy is based on the VXTH index (VIX Tail Hedge), which buys 30 delta VIX calls with 1% of the portfolio when volatility is low, and allocates the rest into the SPX index. Looking at the performance of the index below, three things are immediately clear:
- VXTH did well, but not stellar, in 2008-2009
- VXTH slightly underperformed the benchmark during the bull market of 2010-2020
- VXTH absolutely skyrocketed during the COVID crash of 2020. I think this played right into the strengths of the hedging program: a rapid VIX spike, followed by quick recovery of SPX.
We’re going to look at replicating the VXTH index and extending the methodology to other portfolios, including a leveraged ETF portfolio holding UPRO and TMF.
Equity curves of VXTH (green) compared to SPX (black) from 2006-2020.
How does VXTH work?
The methodology is simple. Each month, the look at the front month VIX futures contract and decide how to allocate to the hedge. With the specified fraction of the portfolio, buy 30 delta VIX calls with one month to expiration.
| VIX future value | Portfolio allocation |
|---|---|
| X <= 15 | 0% |
| 15 > X <= 30 | 1% |
| 30 > X <= 50 | 0.5% |
| X > 50 | 0% |
N.B. The phrase “forward value of VIX” on the CBOE website is strange and doesn’t have an explicit meaning (at least to me). I confirmed the index is looking at the front month VIX future rather than spot VIX by examining the trade log on the CBOE website.
Why hedge with VIX calls?
I think the main reason for using VIX calls as a tail risk hedge is the convexity embedded in the option. In times of low vol, the calls are cheap, and a 1% allocation can buy your portfolio many many OTM calls. But when tail risks come to fruition and VIX spikes like it did in March 2020, the value of the options goes parabolic. If you have the hedge on before everyone else in the market is trying to hedge, you’re in a great position. VIX options are also very liquid in a crisis, in times when other instruments can be illiquid and difficult to unwind for big positions.
Replicating the VXTH index
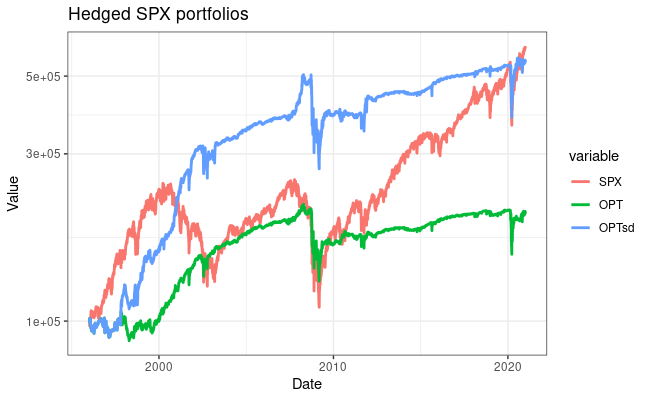
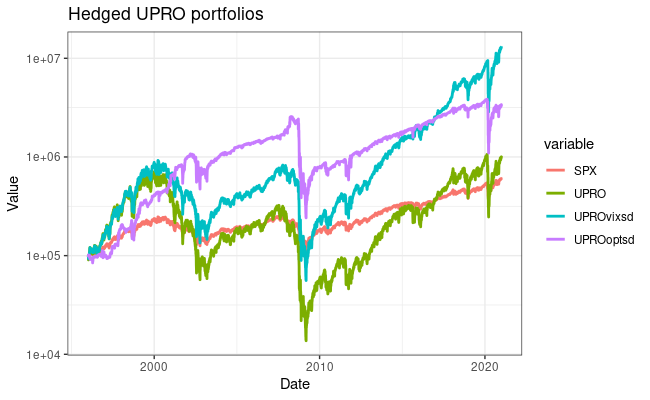
Similar to the last post, I obtained VIX option data from IvyDB and historicaloptiondata.com. /VX prices were obtained from the Quandl continuous futures dataset. Backtesting was done with a custom R program. Option transactions occur at the midpoint of the bid/ask spread and have no transaction costs (big caveat here!). I first replicated VXTH, and equity curves are below. However, I’m still experiencing some tracking error compared to the benchmark, especially in 2020. I think this could be due to differences in my price data or timing luck (see the future directions section). Still, the VXTH replication captures most of the movement of the benchmark and has no drawdown in March 2020.
Equity curves for my replicated VXTH (red) compared to the benchmarks.
Extension to a UPRO/TMF portfolio
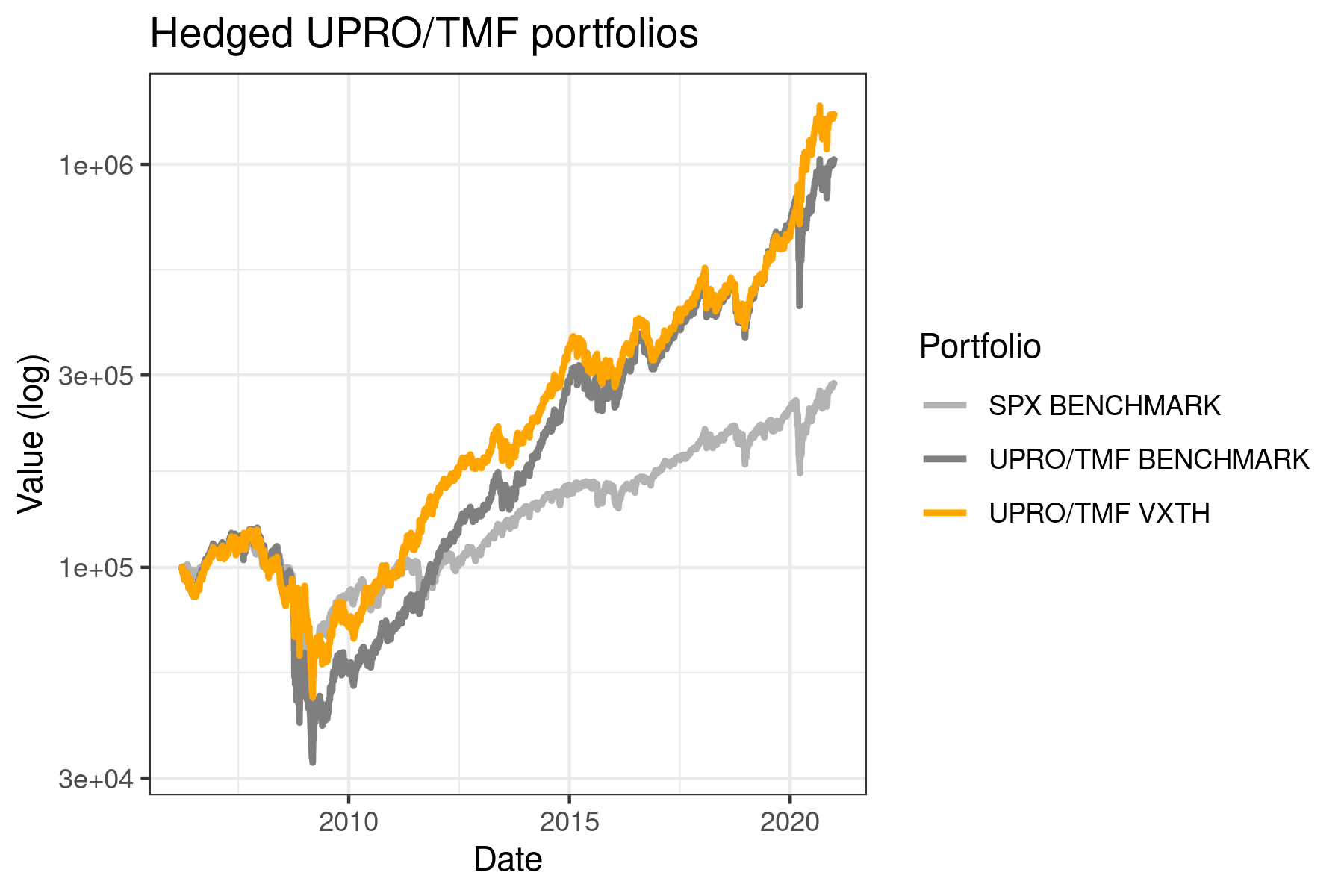
How does adding a VIX call hedge deal with the added volatility of a leveraged portfolio? Quite well! Using the same parameters and a portfolio of 55% UPRO, 45% TMF, the equity curves are below. The outperformance in 2020 isn’t very visible on the log scale, but the VIX call hedged portfolio ends the backtest with a 30% higher balance. The stats on the hedged portfolio are also excellent – improved total and risk-adjusted return, and a comparable drawdown to holding SPX alone. So far, this looks really good!
Equity curves of hedged UPRO/TMF portfolio compared to benchmarks
| SPX | VXTH (benchmark) | VXTH (replicated) | UPRO/TMF | UPRO/TMF + VXTH | |
|---|---|---|---|---|---|
| CAGR | 7.49 | 12.2 | 8.8 | 17.1 | 19.2 |
| Sharpe ratio (Annualized) | 0.49 | 0.67 | 0.66 | 0.70 | 0.87 |
| StdDev (Annualized) | 15.2 | 18.3 | 13.5 | 25.0 | 22.4 |
| Worst drawdown | 52.5% | 37.4% | 35.1% | 70.9% | 57.2% |
Conclusions
Adding a small, constant allocation to VIX calls can improve the absolute and risk-adjusted returns of a portfolio of stocks or leveraged stocks/bonds, at least in the period I backtested. This method is relatively simple compared to the 4 option method I tested in the last post, and only requires management once per month, which can coincide with a monthly portfolio rebalance. There are a few optimizations I want to test before running this method live. I also need to include transaction costs and slippage into my model.
Future directions
I noticed some timing luck in replicating VXTH, specifically around the COVID crash. Slightly changing the days to expiration of the calls would result in very different outcomes, because the VIX calls could be held through the entire crash instead of sold at the “right” time. I think that’s part of why VXTH did so well in March – the VIX peak was right at an option expiration, so the position was exited at just the right time. Ideally we’d strive eliminate this timing luck from a portfolio. I can see a few ways to do this, that I’ll think about implementing in my backtests:
- Instead of holding to expiration, positions should be dynamically opened or closed when VIX crosses one of the allocation thresholds.
- Holding a “ladder” of calls with different expirations to reduce the effect of timing.
- Daily rebalancing (probably not a good idea in practice because of transaction costs).
I want to optimize some other parameters, while being wary of the possibility of overfitting to the relatively few “tail risk” events that have happened in my dataset.
- Allocation amounts (probably more hedge is better with the leveraged portfolio)
- Hedge thresholds. Analyzing the transition matrix from one VIX state to the next may help with this.
- Option delta. Lower delta options will give you more convexity when the rare crashes happen, but you may not benefit from small VIX spikes.
